Flow Matching and Continuous Normalizing Flows

This post explores Flow-based Models, Continuous Normalizing Flows (CNFs), and Flow Matching (FM). We discuss Normalizing Flows, derive the conditional flow matching objective, and examine special instances including diffusion models and optimal transport.

Overview

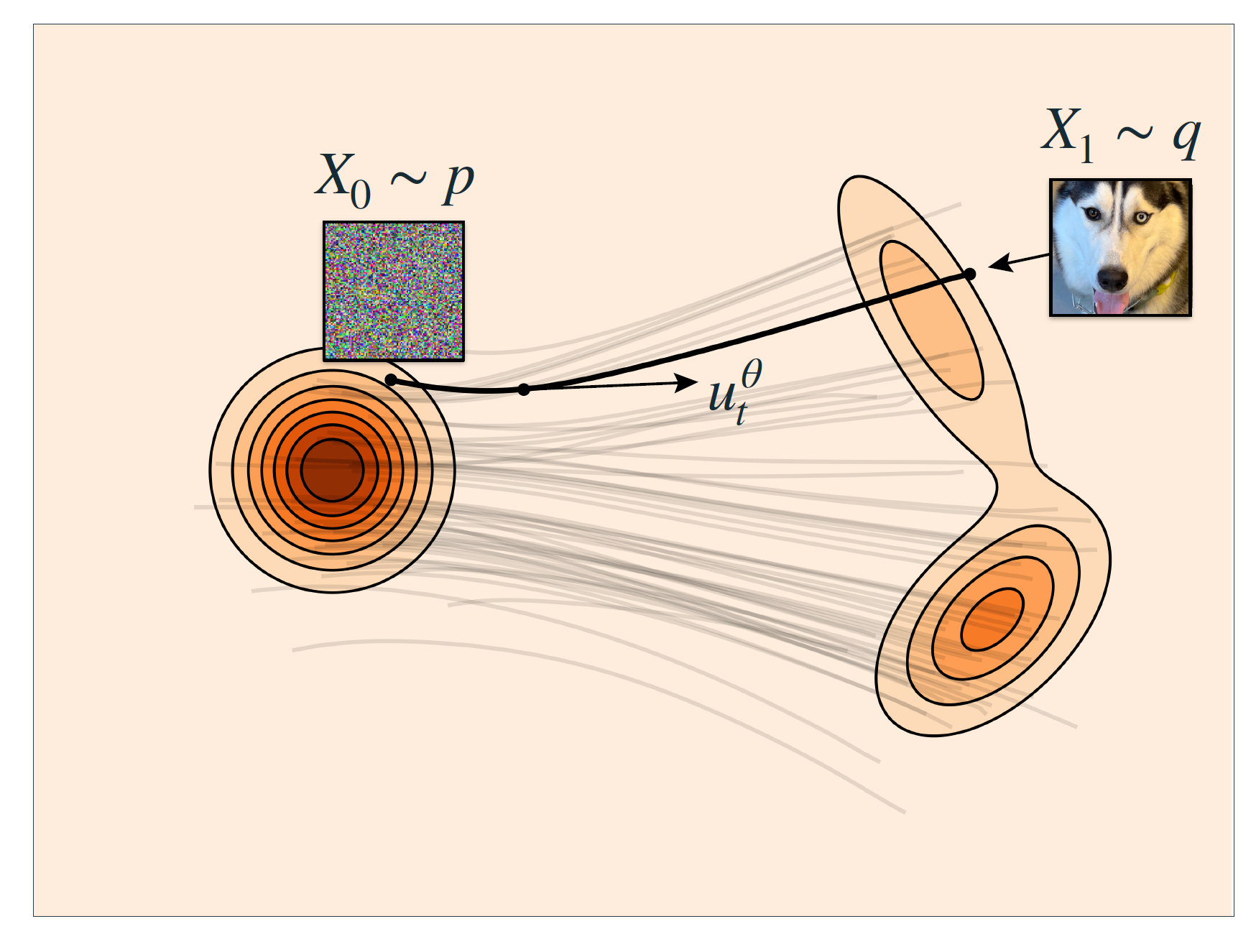
Flow-based Models are generative models based on Normalizing Flows (NFs), which transform complex probability distributions into simple ones through a series of probability density function transformations, and generate new data samples through inverse transformations. Continuous Normalizing Flows (CNFs) extend Normalizing Flows by using ordinary differential equations (ODEs) to represent continuous transformation processes for modeling probability distributions.

Flow Matching (FM) is a method for training Continuous Normalizing Flows that trains the model by learning Vector Fields associated with probability paths, and uses ODE solvers to generate new samples.

Diffusion models are a special case of Flow Matching applications. Using FM can improve their training stability. Furthermore, constructing probability paths using Optimal Transport techniques can further accelerate training speed and enhance model generalization ability.

Normalizing Flows

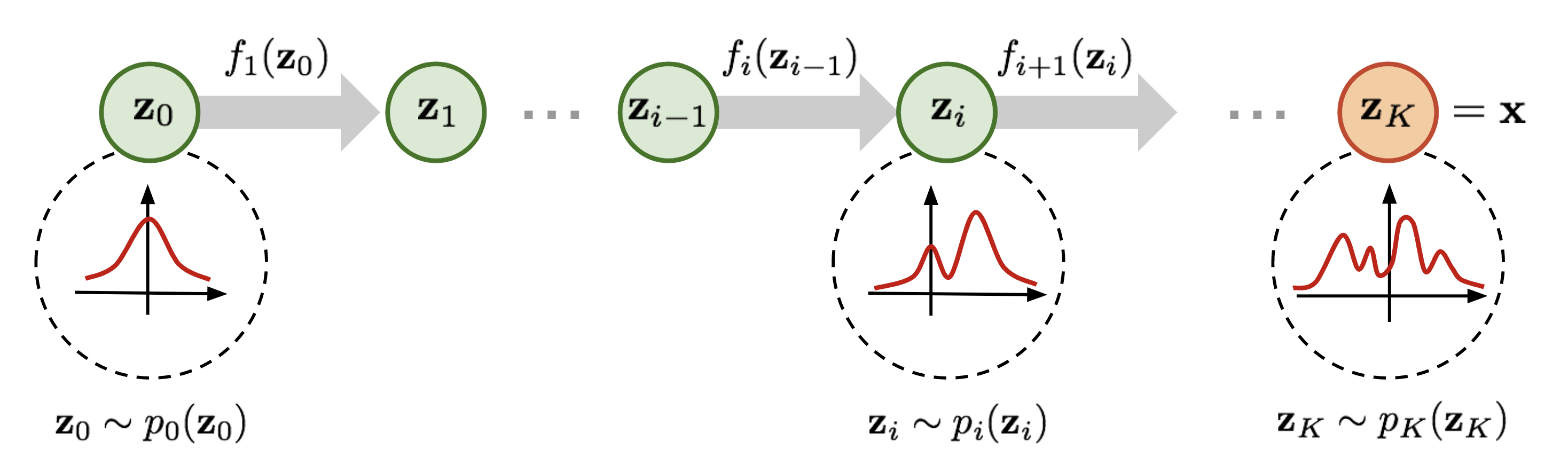
Normalizing Flows (NFs) are invertible probability density transformation methods whose core idea is to progressively transform a simple distribution (typically a Gaussian distribution) into a complex target distribution through a series of invertible transformation functions. This process can be viewed as an iterative sequence of variable substitutions, where each substitution follows the change of variables principle for probability density functions. Through this approach, Normalizing Flows can precisely compute the probability density of the transformed distribution, thereby achieving an exact mapping from simple to complex distributions.

Let $p_0(\mathbf{z_0})$ be the original simple distribution (e.g., standard Gaussian distribution). Normalizing Flows aim to transform it into the target distribution $p(x)$ through a series of invertible transformations $f_i$. These transformations define a mapping from $z_0$ to $x$, and each transformation $f_i$ has its inverse transformation $f_i^{-1}$. Thus, the transformation process can be represented as:

\[x=z_K=f_K\circ f_{K-1}\circ\cdots\circ f_1(z_0)\]

For the $i$-th step, we have:

\[\mathbf{z}_{i-1} \sim p_{i-1}(\mathbf{z}_{i-1})\\ \mathbf{z}_i = f_i(\mathbf{z}_{i-1}), \quad \text{thus } \mathbf{z}_{i-1} = f_i^{-1}(\mathbf{z}_i)\]

According to the change of variables formula for probability density functions, we obtain:

\[\begin{align*} p_i(\mathbf{z}_i) &= p_{i-1}(f_i^{-1}(\mathbf{z}_i)) \left| \det \left( \frac{d f_i^{-1}}{d \mathbf{z}_i} \right) \right|\\ &= p_{i-1}(\mathbf{z}_{i-1}) \left| \det \left( \frac{d f_i}{d \mathbf{z}_{i-1}} \right)^{-1} \right|\\ &= p_{i-1}(\mathbf{z}_{i-1}) \left| \det \left( \frac{d f_i}{d \mathbf{z}_{i-1}} \right) \right|^{-1} \end{align*}\]

The log-likelihood is given by:

\[\log p_i(x)=\log p_{i-1}(z_{K-1})-\log\bigg|\det\frac{df_i}{dz_{i-1}}\bigg|\]

Thus we have

\[\log p(x)=\log \pi_0(z_0)-\sum\limits_{i=1}^{K}\log\bigg|\det\frac{df_i}{dz_{i-1}} \bigg|\]

When this series of transformation functions $f_i$ are invertible and the Jacobian matrices are tractable to compute, during model training, the optimization objective is the negative log-likelihood:

\[\mathcal L(\mathcal D)=-\frac{1}{\mathcal D}\sum_{x\in\mathcal D}\log p(x)\]

Expressive Power of Flow-Based Models

We consider whether we can transform a simple distribution $p(u)$ into any arbitrary probability distribution $p(x)$. Assume $x$ is a $D$-dimensional vector with $p(x)>0$, and the probability distribution of $x_i$ depends only on the previous elements $x_{1:i-1}$. Then we can decompose $p_x(x)$ as a product of conditional probabilities

\[p_x(x)=\prod_{i=1}^{D}p_x(x_i|x_{1:i-1})\]

Assume the transformation $F$ maps $x$ to $z$, where the value of $z_i$ is determined by the cumulative distribution function (CDF) of $x_i$

\[z_i=F_i(x_i,x_{1:i-1})=\int_{-\infty}^{x_i}p_x(x_i'|x_{1:i-1})dx'_i=P(x'_i\le x_i|x_{1:i-1})\]

Clearly, $F_i$ is differentiable, and its partial derivative with respect to $x_i$ equals $p_x(x_i|x_{1:i-1})$. Since the partial derivative of $F_i$ with respect to $x_j~(j>i)$ is 0, $J_F(x)$ is a lower triangular matrix, and thus its determinant equals the product of its diagonal elements, i.e.,

\[\det J_F(x)=\prod_{i=1}^{D}\frac{\partial F_i}{\partial x_i}=\prod_{i=1}^{D}p_x(x_i|x_{1:i-1})=p_x(x)>0\]

Since $p_x(x)>0$, the determinant is also greater than zero, thus the inverse of transformation $F$ must exist. Therefore, we have

\[p_z(z)=p_x(x)|\det J_F(x)|^{-1}=1\]

i.e., $z$ follows a uniform distribution $[0,1]^D$ in $D$-dimensional space.

From the above discussion, we can see that we can transform any distribution into a uniform distribution, and also transform a uniform distribution into any distribution. Thus, through normalizing flows, we can achieve mutual transformation between any two distributions.

Continuous Normalizing Flows

Continuous Normalizing Flows (CNFs) are an extension of Normalizing Flows that can better model complex probability distributions. In traditional Normalizing Flows, transformations are typically defined through a series of invertible discrete functions, whereas in CNFs, these transformations are continuous, enabling the model to adapt more smoothly to data distributions and enhancing the model’s expressive power.

In the continuous setting, FM can be formalized as follows:

• Trajectory

  A trajectory is a mapping from time to sample position. The input is $t$, and the output is $X_t$. The domain of $t$ is $[0,1]$, and the domain of $X_t$ is $\mathbb R^d$

  \[X:[0,1]\to \mathbb R^d,\quad t\to X_t\]

  At $t=0$, $X_0$ comes from a simple initial distribution $p_{init}$. At time $t=1$, we want $X_1$ to follow the true data distribution $p_{data}$.

• Vector Field

  A vector field is a mapping from position and time to instantaneous velocity. The inputs are location and time, and the output is velocity.

  \[u:\mathbb R^d\times[0,1]\to \mathbb R^d,\quad (x,t)\to u_t(x)\]

  At any position $x$ and any time $t$, the vector field provides the direction and speed of sample transformation.

• ODE

  The trajectory $X_t$ must satisfy the following initial value problem:

  \[\frac{d}{dt}X_t=u_t(X_t),\quad X_0=x_0\]

  Here, $x_0\sim p_{init}$ is a sample from the initial simple distribution.

  Solving an ordinary differential equation means finding a curve $X_t$ such that its tangent velocity at each time $t$ exactly equals the value of the vector field $u_t$ at its position (i.e., the derivative of $X_t$ equals $u_t$). That is, solving this differential equation yields the path starting from $x_0$.

• Flow

  A flow is a mapping of the evolution of the initial point $x_0$ at each time, denoted as

  \[\psi_t(x_0)=X_t\]

  with domain $\psi:\mathbb R^d\times[0,1]\to \mathbb R^d,\quad (x_0,t)\to X_t$

  • The flow tells us the position of the sample at time $t$ starting from $X_0=x_0,t=0$, i.e., what $X_t$ is.

  • The flow is the solution satisfying the above ODE: \(\frac{d}{dt}\psi_t(x_0)=u_t(\psi_t(x_0)),~\psi_0(x_0)=x_0\)

In practice, when using CNFs, we need to first estimate the vector field $u_t(x)$, which can be approximated by a neural network $u_t^{\theta}$. After obtaining the approximation $u_t^{\theta}$, we solve the corresponding ODE to get the trajectory $\psi_t^{\theta}(X_0)$.

We want the sample distribution to exactly match $p_{data}$ when the model evolves to the endpoint $t=1$:

\[X_1=\psi_1^{\theta}(X_0)\sim p_{data}\]

Generally, we train $\theta$ through Flow Matching to make the evolved distribution consistent with the data distribution, i.e., to have the endpoint $X_1$ of the trajectory follow the $p_{data}$ distribution.

After learning the vector field $u_t^{\theta}$, we need to numerically solve the $ODE$ (using first-order Euler method) to obtain $X_t$:

\[X_{t+h}=X_t+hu_t^{\theta}(X_t)\]

Below, we will focus on introducing the Flow Matching technique.

Flow Matching

An intuitive method for training Continuous Normalizing Flows is to obtain the distribution of $x_1$ by solving the ODE given initial condition $x_0$, and then constrain it to match the true data distribution using a divergence minimization measure (such as KL divergence). However, since intermediate trajectories are numerous and unknown, inferring $x_1$ (through sampling or computing likelihood) requires repeated ODE simulations, resulting in enormous computational cost. To address this, the paper proposes a new method called Flow Matching (FM).

Flow Matching is a technique suitable for training Continuous Normalizing Flows that is Simulation-Free, meaning it does not require ODE inference of the target data distribution. Its core idea is to ensure that the dynamic characteristics between the model-predicted vector field and the vector field describing the actual motion of data points remain consistent, thereby ensuring that the final probability distribution obtained through CNFs transformation matches the expected target distribution.

Specifically, given a target probability density path $p_t(x)$ and its corresponding vector field $u_t(x)$, where the probability density path $p_t(x)$ is generated by this vector field $u_t(x)$, and $v_t(x)$ is the vector field to be learned, the Flow Matching optimization objective can be defined as:

\[\color{red} \mathcal L_{FM}(\theta)=\mathbb E_{t\sim U[0,1],x\sim p_t(x)}\|v_t(x)-u_t(x)\|^2\]

The core of the Flow Matching objective is to minimize this loss function so that its predicted vector field $v_t(x)$ is as close as possible to the actual vector field $u_t(x)$, thereby accurately generating the target probability density path $p_t(x)$.

Continuity Equation

In physics, the Continuity Equation is a partial differential equation that describes the transport behavior of conserved quantities. Under appropriate conditions, mass, energy, momentum, charge, etc., are all conserved quantities, so many transport behaviors can be described using the continuity equation.

\[\frac{\partial \rho}{\partial t}+\nabla \cdot (\rho v)=0\]

where $\rho$ is the fluid density, $v$ is the fluid velocity vector, $\frac{\partial \rho}{\partial t}$ is the rate of change of fluid density over time, and $\nabla \cdot (\rho v)$ is the divergence of the mass flux density. The meaning of this equation is: the rate of mass change within any closed volume in the fluid equals the difference between the mass flux flowing in and out of that space.

By analogy to probability distributions, this equation can be written as:

\[\color{red}\frac{\partial p_t(x)}{\partial t}+\nabla \cdot (p_t(x)v_t(x))=0\]

In the above equation, $p_t(x)$ is the probability density function at time $t$, and $v_t(x)$ is the vector field associated with $p_t(x)$. This equation is a necessary and sufficient condition for the vector field $v_t(x)$ to generate the probability density path $p_t(x)$, and will be used as a constraint in subsequent derivations.

For conditional probability, the above equation becomes

\[\frac{\partial p_t(x|x_1)}{\partial t}+\nabla \cdot (p_t(x|x_1)v_t(x|x_1))=0\]

Conditional and Marginal Probability Paths and Vector Fields

Since we need to predetermine appropriate $p_t(x)$ and $u_t(x)$ during training, this is obviously difficult. However, we can start from the true distribution $q(x_1)$ and transform the true distribution into other simple distributions through invertible transformations. In this process, we can explicitly write out the conditional probability path $p_t(x|x_1)$, and according to the Continuity Equation, we can derive the conditional vector field. By weighting the conditional vector field and conditional probability path (density) using Bayes’ formula, we can recover the marginal probability path and marginal vector field, namely $p_t(x)$ and $u_t(x)$.

Since the marginal density is the integral of the conditional density:

\[p_t(x)=\int p_t(x|x_1)q(x_1)dx_1\]

Thus, its partial derivative with respect to $t$ is:

\[\frac{\partial p_t(x)}{\partial t}=\int \frac{\partial p_t(x|x_1)}{\partial t}q(x_1)dx_1=-\int \nabla \cdot (p_t(x|x_1)u_t(x|x_1))q(x_1)dx_1\]

According to the continuity equation, if we want a vector field $u_t(x)$ to correspond to the probability path $p_t(x)$, then we must have:

\[-\nabla \cdot (p_t(x)u_t(x))=-\int \nabla \cdot (p_t(x|x_1)u_t(x|x_1))q(x_1)dx_1\]

We can solve to get

\[\color{red}u_t(x)=\int u_t(x|x_1)\frac{p_t(x|x_1)}{p_t(x)}q(x_1)dx_1\]

This means that if the marginal vector field $u_t(x)$ is given by the above equation, then it will correspondingly generate the marginal probability path $p_t(x)$.

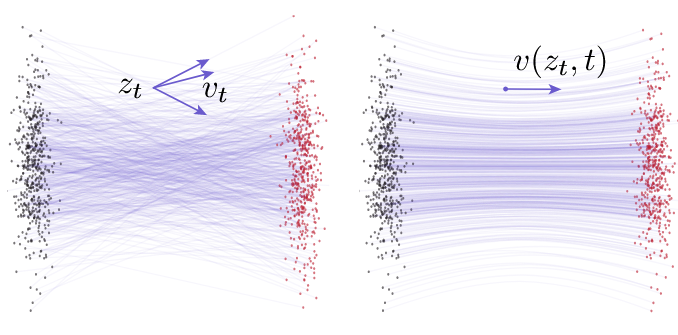
As shown in the figure above, computing the marginal vector field essentially performs a weighted average over all possible conditional vectors.

Conditional Flow Matching

We find that even though we have the formula for computing $u_t(x)$, the above marginal integral is still intractable, so directly optimizing the Flow Matching objective function is infeasible.

The paper proposes the Conditional Flow Matching method. As long as $u_t(x|x_1)$ and $u_t(x)$ satisfy the above weighted marginal integral condition, the Conditional Flow Matching optimization objective has the same optimal solution as the original Flow Matching objective function. The Conditional Flow Matching optimization objective is:

\[\color{red} \mathcal L_{CFM}(\theta)=\mathbb E_{t\sim U[0,1],x_1\sim q(x_1),x\sim p_t(x|x_1)}\|v_t(x)-u_t(x|x_1)\|^2\]

The paper proves through Theorem1 that the Conditional Flow Matching optimization objective and the original Flow Matching objective function have the same gradient, which means they have the same optimal solution.

Theorem1 Assume that for all $x\in\mathbb R^d$ and $t\in [0,1]$, we have $p_t(x)>0$. Then $\mathcal L_{CFM}$ and $\mathcal L_{FM}$ differ by a constant independent of $\theta$, i.e.,

\[\nabla _{\theta}\mathcal L_{FM}(\theta)=\nabla _{\theta}\mathcal L_{CFM}(\theta)\]

Proof

To ensure the existence of integrals and to facilitate exchanging the order of integration (using Fubini’s theorem), we assume that $q(x)$ and $p_t(x_1)$ decay to 0 sufficiently fast as $|x|\to\infty$, and that $u_t$, $v_t$, $\nabla v_t$ are all bounded.

First, we expand the squared norm:

\[\begin{align*} \|v_t(x) - u_t(x)\|^2 &= \|v_t(x)\|^2 - 2 \langle v_t(x), u_t(x) \rangle + \|u_t(x)\|^2 \\ \|v_t(x) - u_t(x \mid x_1)\|^2 &= \|v_t(x)\|^2 - 2 \langle v_t(x), u_t(x \mid x_1) \rangle + \|u_t(x \mid x_1)\|^2 \end{align*}\]

Next, note that $u_t$ is independent of $\theta$, and we have:

\[\begin{align*} \mathbb{E}_{p_t(x)} \|v_t(x)\|^2 &= \int \|v_t(x)\|^2 p_t(x) dx \\ &= \iint \|v_t(x)\|^2 p_t(x \mid x_1) q(x_1) dx_1 dx \\ &= \mathbb{E}_{q(x_1), p_t(x \mid x_1)} \|v_t(x)\|^2 \end{align*}\]

Next, we compute:

\[\begin{align*} \mathbb{E}_{p_t(x)} \langle v_t(x), u_t(x) \rangle &= \int \left\langle v_t(x), \int u_t(x \mid x_1) \frac{p_t(x \mid x_1) q(x_1)}{p_t(x)} dx_1 \right\rangle p_t(x) dx \\ &= \int \left\langle v_t(x), \int u_t(x \mid x_1) p_t(x \mid x_1) q(x_1) dx_1 \right\rangle dx \\ &= \iint \langle v_t(x), u_t(x \mid x_1) \rangle p_t(x \mid x_1) q(x_1) dx dx_1 \\ &= \mathbb{E}_{q(x_1), p_t(x \mid x_1)} \langle v_t(x), u_t(x \mid x_1) \rangle \end{align*}\]

Meanwhile, we note that the third term in the squared norm expansion is a constant independent of $\theta$, thus proving the theorem.

Based on the above discussion, the core of constructing a trainable flow model becomes how to design appropriate conditional probability paths and conditional vector fields. Generally speaking, conditional probability paths are easier to construct, while conditional vector fields are more challenging. According to the Continuity Equation, we know

\[\frac{\partial p_t(x|x_1)}{\partial t}+\nabla \cdot (p_t(x|x_1)v_t(x|x_1))=0\]

This equation allows us to explicitly compute a closed-form $v_t(x|x_1)$ when $p_t(x|x_1)$ is a Gaussian family or a simple function.

Calculate Conditional Probability Paths and Conditional Vector Fields

Conditional Flow Matching can choose arbitrary conditional probability paths as long as they satisfy boundary conditions. Here, for simplicity (to obtain a closed-form conditional vector field), we analyze how to construct $p_t(x|x_1)$ and $u_t(x|x_1)$ for general Gaussian conditional probability paths.

Assume the conditional probability path is a Gaussian probability path:

\[p_t(x|x_1)=\mathcal N(x|\mu_t(x_1),\sigma_T(x_1)^2I)\]

We impose the following constraints on this conditional probability path:

At the beginning of time ($t=0$), we satisfy $\mu_0(x_1) = 0, \sigma_0(x_1) = 1$, ensuring that all conditional probability paths converge to the same standard Gaussian noise distribution, i.e., $p(x) = \mathcal{N}(x \mid 0, I)$.

At the end of time ($t=1$), we satisfy $\mu_1(x_1) = x_1, \sigma_1(x_1) = \sigma_{\min}$, where $\sigma_{\min}$ should be set sufficiently small to ensure that $p(x \mid x_1)$ is a Gaussian distribution with mean $x_1$ and small variance, so that the conditional probability path converges near $x_1$.

This setting defines a deterministic transformation process, starting from a standard Gaussian distribution at $t=0$ and gradually transforming to the target distribution at $t=1$.

For a probability path, there exist infinitely many vector fields that can generate it, for example, by adding a divergence-free component to the Continuity Equation, but this leads to unnecessary computational cost. Here we can use the simplest vector field, which corresponds to the standard transformation of a Gaussian distribution, with the corresponding data point Flow Map being:

\[x_t=\psi_t(x)=\sigma_t(x_1)x+\mu_t(x_1)\]

where $x\sim\mathcal N(0,1)$. $\psi_t(x)$ is an affine transformation that maps $x$ to a normal random variable with mean $\mu_t(x_1)$ and standard deviation $\sigma_t(x_1)$. That is, according to Equation 4, $\psi_t$ pushes the noise distribution $p_0(x|x_1) = p(x)$ to $p_t(x|x_1)$, i.e.,

\[\begin{equation} [\psi_t]_∗ p(x) = p_t(x|x_1). \end{equation}\]

The flow further defines a vector field that generates the conditional probability path:

\[\begin{equation} \frac{d}{dt} \psi_t(x) = u_t(\psi_t(x) \mid x_1). \end{equation}\]

Reparametrizing $p_t(x|x_1)$ in terms of $x_0$ and substituting into Equation (13), we obtain the CFM loss function as follows:

\[\begin{equation} \mathcal{L}_{\text{CFM}}(\theta) = \mathbb{E}_{t, q(x_1), p(x_0)} \left\| v_t(\psi_t(x_0)) - \frac{d}{dt} \psi_t(x_0) \right\|^2. \end{equation}\]

Since $\psi_t$ is a simple (invertible) affine mapping, we can utilize Equation (13) to obtain a closed-form solution for $u_t$. Let $f’$ denote the derivative with respect to time $t$, i.e., $f’ = \frac{d}{dt} f$, where $f$ is a time-dependent function.

Theorem2 Let $p_t(x|x_1)$ be the Gaussian probability path as defined in Equation 10, and $\psi_t$ be its corresponding flow map as described in Equation 11. Then the vector field that uniquely defines $\psi_t$ has the following form:

\[u_t(x|x_1) = \frac{\sigma'_t(x_1)}{\sigma_t(x_1)} \left( x - \mu_t(x_1) \right) + \mu'_t(x_1)\]

Therefore, $u_t(x|x_1)$ generates the Gaussian path $p_t(x|x_1)$

Proof:

For notational brevity, let $w_t(x) = u_t(x|x_1)$. Now consider Equation 1:

\[\frac{d}{dt}\psi_t(x) = w_t(\psi_t(x)).\]

Since $\psi_t$ is invertible (because $\sigma_t(x_1) > 0$), we set $x = \psi_t^{-1}(y)$ and obtain

\[\psi_t'(\psi_t^{-1}(y)) = w_t(y)\]

Here we use prime notation to denote derivatives, emphasizing that $\psi_t’$ is evaluated at $\psi_t^{-1}(y)$.

Now, inverting $\psi_t(x)$ yields

\[\psi_t^{-1}(y) = \frac{y - \mu_t(x_1)}{\sigma_t(x_1)}.\]

Taking the derivative of $\psi_t$ with respect to $t$ yields

\[\psi_t'(x) = \sigma_t'(x_1)x + \mu_t'(x_1).\]

Substituting these last two equations into the second line, we obtain

\[w_t(y) = \frac{\sigma_t'(x_1)}{\sigma_t(x_1)}(y - \mu_t(x_1)) + \mu_t'(x_1).\]

Special Instances of Gaussian Conditional Probability Paths

Diffusion conditional VFs

Variance Exploding (VE) and Variance Preserving (VP) in diffusion models are two different types of diffusion processes used in generative models to simulate two different data distribution change processes.

Variance Exploding (VE)

The VE diffusion model is a diffusion process that increases data variance during the generation process. In this model, as time progresses, data samples gradually become more noisy, with variance continuously increasing until reaching a stable state. A characteristic of the VE process is that it allows the model to explore a wider latent space when generating data, which helps generate diverse samples.

The conditional probability path for VE is:

\[p_t(x | x_1) = \mathcal{N}(x | x_1, \sigma_{1-t}^2 I)\]

where $\sigma_t$ is an increasing function, $\sigma_0 = 0, \sigma_1 \gg 1$, corresponding to mean and standard deviation

\[\mu_t(x_1) = x_1, \quad \sigma_t(x_1) = \sigma_{1-t}\]

According to Theorem 3, the conditional vector field can be computed as:

\[u_t(x | x_1) = - \frac{\sigma'_{1-t}}{\sigma_{1-t}}(x - x_1)\]

Variance Preserving (VP)

The VP diffusion model is a diffusion process that keeps data variance constant during the generation process. In this model, the variance of data samples remains constant throughout the generation process, meaning that while the model introduces noise, it also reduces noise in some way to maintain the overall variance of the data. VP models are typically used in application scenarios that require maintaining data distribution stability, such as maintaining image clarity and structural features in image generation.

The conditional probability path for VP is:

\[p_t(x | x_1) = \mathcal{N}\left(x \mid \alpha_{1-t}x_1, (1 - \alpha_{1-t}^2)I\right) \text{, where } \alpha_t = e^{-\frac{1}{2}T(t)}, T(t) = \int_0^t \beta(s)ds\]

where $\alpha, \beta$ are noise schedule functions, corresponding to mean and standard deviation

\[\mu_t(x_1) = \alpha_{1-t}x_1, \quad \sigma_t(x_1) = \sqrt{1 - \alpha_{1-t}^2} \,。\]

According to Theorem 3, the conditional vector field can be computed as:

\[\begin{align*} u_t(x | x_1) &= \frac{\alpha'_{1-t}}{1-\alpha_{1-t}^2}(\alpha_{1-t}x - x_1) \\ &= -\frac{T'(1-t)}{2}\left[ \frac{e^{-T(1-t)}x - e^{-\frac{1}{2}T(1-t)}x_1}{1-e^{-T(1-t)}} \right] \end{align*}\]

Optimal Transport conditional VFs

Optimal Transport (OT) chooses to define the mean and standard deviation of the conditional probability path as simple linear functions. As time $t: 0 \to 1$, corresponding to the probability density path from $p(x) = \mathcal{N}(x | 0, I)$ to $p_1(x | x_1)$, the mean and standard deviation are defined as:

\[\mu_t(x_1) = tx_1, \quad \text{and} \quad \sigma_t(x_1) = 1 - (1 - \sigma_{\min})t\]

Then the corresponding Flow Map is:

\[\psi_t(x) = (1 - (1 - \sigma_{\min})t)x + tx_1\]

According to Theorem 3, the closed-form solution of the conditional vector field can be computed as:

\[u_t(x | x_1) = \frac{x_1 - (1 - \sigma_{\min})x}{1 - (1 - \sigma_{\min})t}\]

Optimal transport paths are straight lines, whereas diffusion paths are curves, thus achieving faster training and generation speeds, as well as better performance.